Versuch
Info


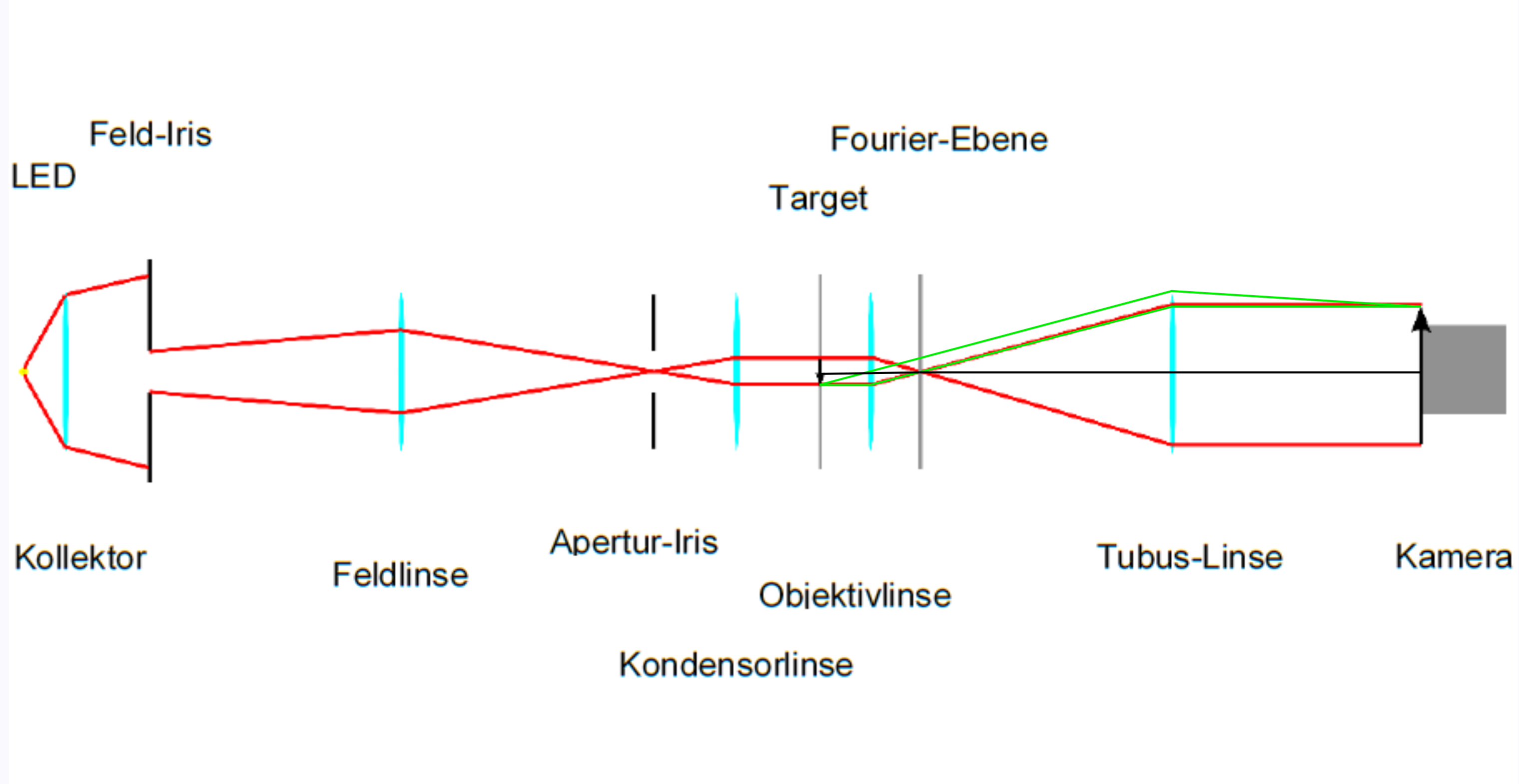
Bei dem Aufbau handelt es sich um ein 4f-Mikroskop mit einem senkrechten Arm hinter der Objektivlinse. Dieser ermöglicht, außer dem Bild des Objekts gleichzeitig auch das Fourier-transformierte Muster, welches durch das Objekt (Target) erzeugt wird, zu beobachten. Mit einem Spalt, einer Irisblende oder einer anderen Maske kann man das Fourier-transformierte Muster filtern und dann sehen, wie sich die Manipulation auf das Bild auswirkt.
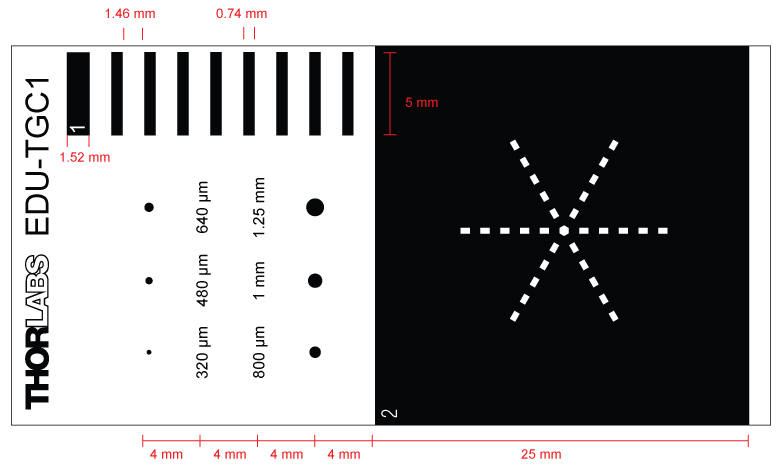
Zur Demonstration des Babinet’schen Theorems wird ein Dreieck-Gitter verwendet. Die schwarzen Dreiecke haben die gleichen Abmessungen wie die transparenten. Wird die nullte Ordnung durch einen Punkt auf der Maske blockiert, dann sehen beide Strukturen im Kamerabild identisch aus und können nicht unterschieden werden.
Beschreibung
Das Babinet’schen Theorem besagt, dass die Beugungsbilder zweier komplementärer Strukturen bis auf die nullte Ordnung identisch sind. Mit Ausblendung der nullten Ordnung wird die Helligkeitsverteilung verändert. Die nullte Beugungsordnung trägt aber keinerlei Strukturinformation. Die Strukturinformationen (Dreieckswinkel und -größen) sind in den höheren Beugungsordnungen enthalten und diese sind für alle Dreiecke gleich.
Hinweise zur Durchführung:
Bei dem hier beschriebenen Versuch handelt es sich um Aufgabe 25 auf Seite 94 im Handbuch von Thorlabs.
Um die Sichtbarkeit des gefilterten Bildes zu verbessern, erhöht man in der Kamera-Software den „Gain“.
Hinweise zum Aufbau:
Der Aufbau des 4f-Mikroskops ist im Handbuch von Thorlabs ab Seite 35 beschrieben.
Die ThorCam Kamera Software Version 3.1.1 ist auf dem Surface Notebook installiert.